Obtención
de un Polinomio de Taylor de Orden 2.
f(x) = ex a=0
f(0) = e0 = 1 f ´(0) = e0= 1
En general, podemos aproximar a f(x)
en x=a a polinomios que cumplan con las condiciones siguientes:
Pn(j)(a)
= f(j)(a) con
j=1,2,..,n
donde: f(j)(x) es la
j-ésima derivada de f(x) en x=a. Entonces:
Rn(x)es el resto
probable de la serie cuya fórmula para su cálculo es:
donde z es un número entre a y x ( se llama residuo después de n +1 términos.)
La serie de Taylor se rebautizará "serie
de Maclaurin" para x = 0
Fórmulas
y series de Taylor de funciones elementalesf(x) = ex esta función puede derivarse infinitamente ( derivadas de cualquier orden)
Desarrollemos Taylor para a = 0 ( a en este caso vale cero )
f(0) = e0 = 1, f’(0)
= e0 = 1, f "(0)
= e0 = 1, .... f n(0) = e0 =
1, f
n+1(z) = ez (0 < z < x)
Calculemos ex
para x = 1 hasta n = 6 (grado 6º ) así tenemos:
Para hallar el error
utilizaremos el resto, Rn =
Como tenemos 6 términos para hallar el resto utilizaremos el séptimo, n = 7 de esa manera:

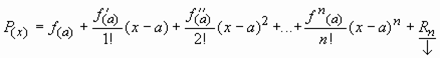




No hay comentarios:
Publicar un comentario